Some context for MF III
- adding some context to MA courses
- The biggest issue with MA is the lack of context imho. What’s the point? Why should I care?
Trigonometry is a shortcut.
- The Art of Problem Solving
- Right triangles are of paramount importance in geometry. Thus, mathematicians have developed a shorthand for writing the ratios of the sides of right triangles. Instead of writing “the ratio of the leg adjacent to an angle to the hypotenuse of the triangle,” we write “cos “. Because expressions of this type frequently come up in physics, engineering, and many other branches of science, you can see why such a shorthand was developed. We’ll start off with a few definitions.
- What use is trigonometry? In a word, it’s a shortcut. Using the trigonometric functions and our knowledge about special right triangles, we can quickly find various side lengths and angle measures. Examples are included among the problems below. Trigonometry also gives us yet another method to prove that two angles are equal. If we know that two acute angles have the same value for some trigonometric function (e.g. ), then we know the angles are equal ( ). (Can you prove this?)
- Can I solve some of the problems in Mathematics via Problems with Rational Trigonometry?
Practice possibilities
In my experience, the only way to successfully teach a more sophisticated technique is to present a problem where known simpler techniques fail.
If you want your students to understand why a more sophisticated definition is preferable, then you have to introduce them to a situation where the simpler definition breaks down and the sophisticated definition saves the day. ~ Justin Skycak
how to learn new concepts
Cast some complicated problem into your chosen programming language/abstract framework and model it yourself, try to reinvent it there.
From Structure and Interpretation of Computer Programs (SICP):
You develop a language (sometimes consisting just of one or two functions) such that the solution of the problem can be trivially expressed in it.
Many problems in computer science become significantly more tractable if you have a tool for expressing your own way of thought, not the way of thought of the machine. You write programs for yourself in the first place. It’s similar to mathematics: when proving a theorem, you prove it (using the language of formal algebra/calculus/etc.) to yourself, trying to figure out the best way to do it, using as little efforts as possible and being elegant.
keywords: language agnostic, domain specific languages
Examples
TODO
How to move past the advanced beginner stage?
The advanced beginner stage is the transition point between the beginner and intermediate stage.
mini-projects
- read Divine Proportions and implement some concepts in Julia
Euler’s formula
Thoughts after 2100 XP (~ 35 hours of work)
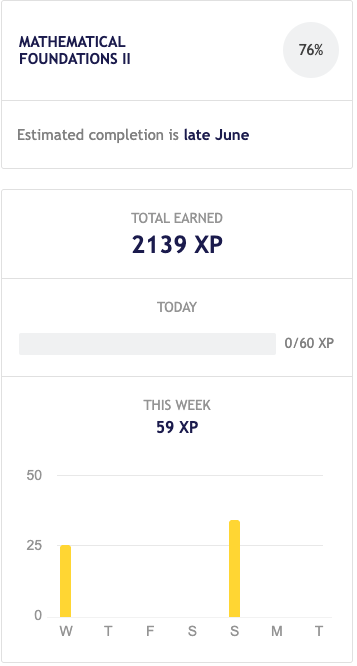
What have I learned? What intrigued me about this process?
I took the diagnostics, still the exercises felt too easy and not challenging enough.
Now, I completed 78% of math foundations II. Maybe it’s time to switch to MF3.
I felt like something was missing.
[ ] remix lessons and make them your own
Update 10.06.2025
I completed 95% of MF2 and 28% of MF3.